5. Sampling issues
Until the late 19th century, audio systems for live and recording applications were designed using acoustical and mechanical tools - such as the walls of a concert hall (amplification, colouring), copper tubes in shipping (short distance transport), grooves on a wax roll picked up by a needle and amplified by a big horn (long distance transport).
In 1872 everything changed when, independently from each other, Emil Berliner and Thomas Edison invented the carbon microphone(*5A), introducing the possibility of transforming acoustic waves to electronic signals.
This was the beginning of the ‘analogue’ era - using electrical circuits to mix, amplify, modify, store and transport audio signals. This era saw the introduction of the electrical Gramophone in 1925 (Victor Orthophonic Victrola*5B), the reel to reel tape recorder in 1935 (AEG’s Magnetophon*5C) and the compact cassette in 1962 (Philips*5D). In the years to follow, large scale live audio systems became available built around mixing consoles from Midas, Soundcraft, Yamaha and others.
5.1 Digital Audio
In 1938, Alec Reeves from ITT patented Pulse Code Modulation (PCM)(*5E), marking the start of the development of digital systems to process and transport audio signals - with the goal to make systems less susceptible for noise and distortion. In 1982, the first album on Compact Disc, developed by Philips and Sony, was released (Billy Joel’s 52nd street) - introducing 16-bit 44.1 kHz PCM digital audio to a broad public(*5F).
The first mass produced Yamaha digital mixing system was the DMP7, launched in 1987 - introducing 16-bit A/D and D/A conversion and Digital Signal Processing (DSP) architecture to small scale music recording and line mixing applications(*5G). But where 16 bits are (only just) enough for CD quality playback, the 90dB typical dynamic range it can reproduce is insufficient for large scale live mixing systems. In 1995, the Yamaha 02R digital mixing console introduced 20-bit A/D and D/A conversion, supporting 105 dB dynamic range(*5H). Matching - or in many cases surpassing - the audio quality of analogue systems at that time, the 02R was the trigger for both the recording and the live audio market to start a massive migration from analogue to digital. Since then, A/D and D/A conversion technologies have matured to 24-bit A/D and D/A conversion and transport, and 32-bit or more DSP architecture, supporting system dynamic ranges of up to 110 dB - far beyond the capabilities of analogue systems(*5I). DSP power has reached levels that support massive functionality that would have been simply not possible with analogue systems.
At the time of writing of this white paper, the majority of investments in professional live audio systems involve a digital mixer. Also, networked distribution systems to connect inputs and outputs to mixing consoles are now replacing digital and analogue multicore connection systems.
All networked audio systems use A/D converters to transform analogue audio signals to the digital domain through the sampling process, and D/A converters to transform samples back to the analogue domain. Assuming that all A/D and D/A converters, and the distribution of the samples through the digital audio system, are linear, sampling does not affect the Response of a digital audio system - all A/D and D/A processes and distribution methods sound the same. (only intended changes - eg. sound algorithm software installed on a system’s DSP’s - affect the sound). Instead, sampling and distribution can be seen as a potential limitation as it affects audio signals within the three audio dimensions: level, frequency and time. This chapter presents the sampling process limitations to a system’s Performance: dynamic range, frequency range and temporal resolution.
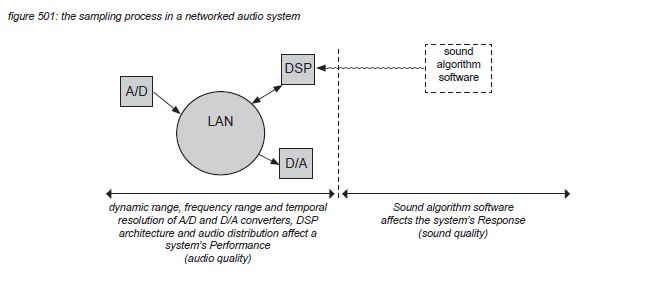
5.2 Dynamic range
A basic signal chain from analogue line input to line output in a networked audio system consists of an A/D converter, a distribution network (LAN), a DSP unit and a D/A converter:
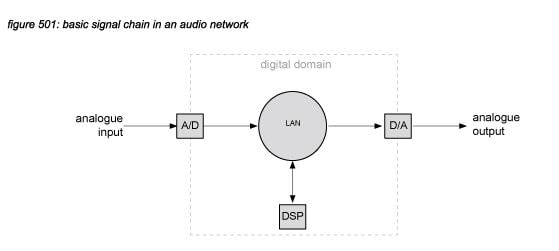
A/D converter circuits are used to sample a continuous analogue (electronic) audio signal at a constant timeinterval, in broadcast and live sound applications normally 20.8 microseconds, corresponding with a sample rate of 48,000 samples per second. Each time interval, the sampling process produces a number to represent the analogue signal using a certain amount of binary digits: the bit depth. For linear A/D converters with a bit depth of 24 bits, the sample can cover 16,777,216 different values. After transport through the audio network and DSP processing, a D/A converter converts the digital samples back to a continuous analogue signal, in most cases with the same sample rate and bit depth.
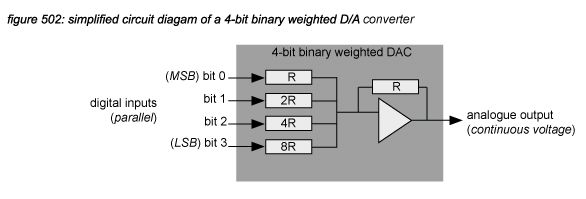
D/A converter circuits basically consist of one or more highly accurate switched current sources producing an analogue output current as a result of a digital input code. To illustrate the basic concept of a D/A converter, an example of a simple 4-bit binary weighed D/A converter is presented in figure 502. The circuit uses individual resistors for each bit, connected to a summing point. Commonly available D/A converters use more complex high speed techniques such as delta-sigma modulation(*5J).
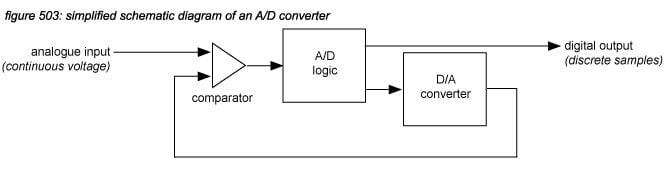
A/D converters are slightly more complex, using an AD logic component driving a D/A converter. The output of the D/A converter is compared to an analogue input, with the result (higher or lower) driving the AD logic component.
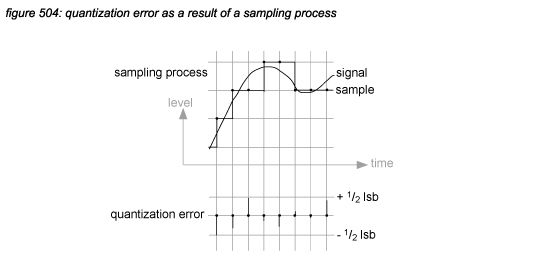
Quantization error
In a digital system’s A/D converter, the sampled waveform can never be represented accurately by the digital samples because the value representation of the least significant bit (LSB) is always a little off by up to plus or minus 1/2 LSB. Similar with A/D conversion, DSP MAC operations (Multiply and Accumulate*5K) and transformations from a high bit depth to a lower bit depth have to be rounded to up to plus or minus 1/2 LSB after each processing step. These errors are called quantization errors.
The level of the quantization error in an A/D converter depends on the sample rate, the bit depth and the sampled waveform. The quantization error in a DSP process depends also on the number of steps. As D/A converters are assumed to reproduce the digital representation of the signal - and not the original signal, they do not generate quantization errors. However, a D/A converter can never reach a higher resolution than 1 LSB. Figure 504 illustrates an A/D converter’s quantization error.
In binary numbers, each bit represents a factor of 2, which corresponds to a ratio of 6.02 dB. Although in reality it is much more complex(*5L), as a rule of thumb for A/D converters and DSP operations, a worst case quantization error noise floor of -6.02 dB times the bit depth is often used.
Linearity error
Ideal A/D and D/A converters use 100% accurate components - but in real life, electronic components always possess a certain tolerance causing nonlinearity. It is assumed that professional A/D and D/A converters possess a linearity error of less than 1 LSB. Digital transport, networked distribution, storage and DSP processes are all digital and therefore don’t generate linearity errors (unless compression is used eg. MP3).
Dynamic range
The internal resolution of dedicated audio DSP chips - the bit depth at which MAC operations are performed in the DSP core - is usually 40 bits or higher, providing enough internal resolution to keep the output of high DSP power algorithms (with many calculations) to stay well above 32 bits. If the audio network protocol used in the system is also 32 bits - eg. Dante in 32-bit mode, the dynamic range of the digital part of a networked audio system can be estimated using the rule of thumb of 6 dB per bit times 32 bits = 192 dB.
As this range is far greater than the theoretical 144 dB dynamic range limit of a system’s A/D and D/A converters, it can be assumed that a system’s dynamic range is mainly limited by just these components. Still, systems available on the market will not reach this value. Electronic circuits such as the power supplies, buffer amps and head amps before the A/D converter, as well as buffer amps and balancing circuits after the D/A converter, add electronic noise to the signal chain. Also, in most designs noise is added intentionally in the digital domain to improve the Performance at very low signal levels (dither)(*5M). A typical dynamic range of a signal chain in a networked audio system - excluding the power amplifier - is 108dB(*5N).
5.3 Frequency range
Where the dynamic range of a signal chain in a networked audio system is mainly determined by the bit depth, the frequency range is mainly determined by the sampling rate.
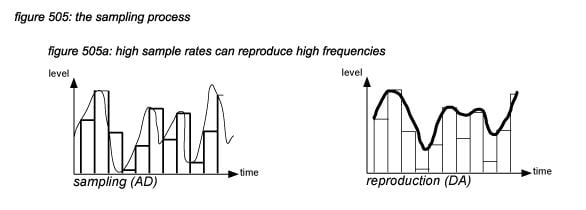
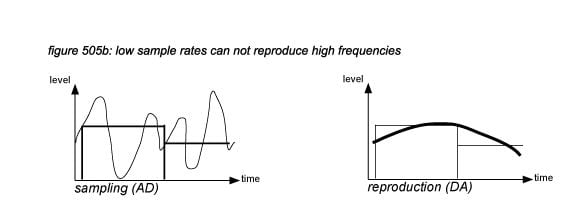
The process of sampling an audio signal every sample interval is visualised in figure 505: the waveform of the audio signal is chopped into discrete samples with a high sample rate (figure 505a) and a low sample rate (figure 505b). It can be assumed that for high frequencies to be reproduced by a sampling system, a high sample rate has to be used. However, a high sample rate implicates that electronic circuits have to be designed to operate with high frequencies, the data transfer and DSP involve a high data rate (bandwidth), and storage requires a high storage capacity. For efficiency reasons, it is necessary to determine exactly how high a sampling rate must be to capture a certain frequency bandwidth of an audio signal, without too much costs for the design of electronic circuits, digital transport, DSP and storage.
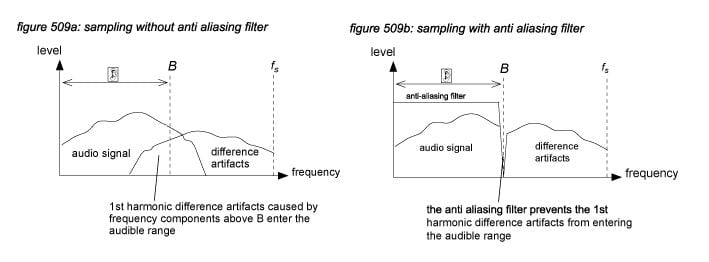
To determine the minimum sampling rate to capture an audio signal’s full bandwidth, figure 506 presents the sampling process both in the time domain and in the frequency domain. The most important observation when looking at the process in the frequency domain is that the sampling signal is a pulse train with a fundamental harmonic at the sampling frequency, and further odd harmonics at 3, 5, 7 etc. times the fundamental frequency. Multiplying the audio waveform with the sample pulse train results in the original waveform, plus sum and difference artefacts around every harmonic of the sample waveform. (Figure 506 only shows the 1st and 3rd harmonic).
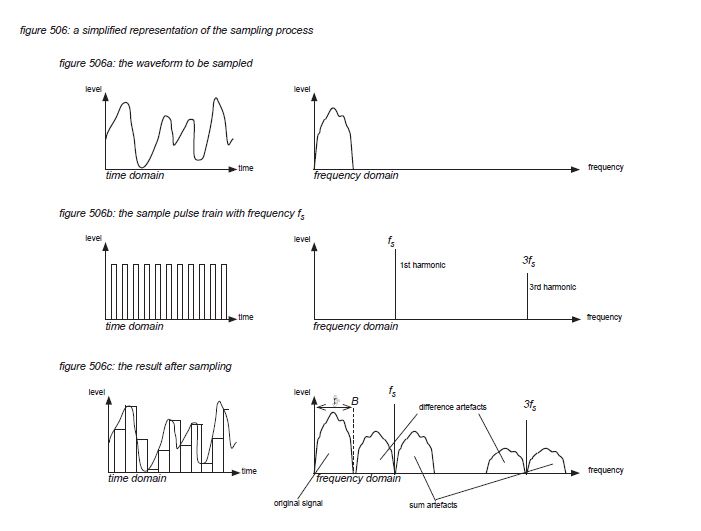
In figure 506c, the human auditory system’s frequency limit is indicated with the dotted line B. If the difference artefact of the 1st harmonic of the sample pulse train at the sample rate fs lies completely above B, then all artefacts fall outside of the hearing range - so the reproduction of the audio signal is accurate inside the boundaries of the audio universe. However, if either the audio signal has a full bandwidth (B) and fs falls below 2B (figure 507a), or if fs is twice the full bandwith B and the audio signal includes frequency components higher than B (figure 507b), the reproduction is no longer accurate because the difference artefacts of the first harmonic fall in the audible range. This phenomenon is called aliasing.
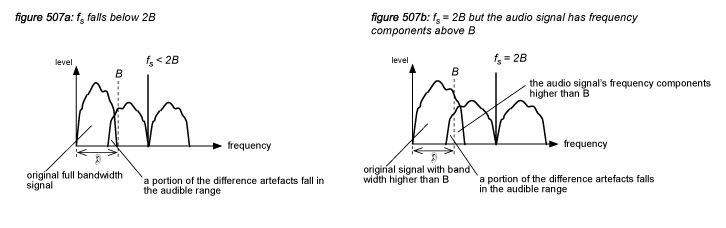
The conclusion is that 1) fs must be at least twice the frequency limit of the human auditory system (20 kHz) to be able to reproduce an accurate audio signal, and 2) the bandwidth of the audio signal must be less than half of fs . The second conclusion is called the Nyquist-Shannon sampling theorem(*5O).
The first conclusion leads to the system design parameter of selecting a sample frequency of at least 40 kHz to allow an accurate representation of signals up to the hearing limit of 20 kHz. But the second conclusion makes it very difficult to do so, because most audio signals that come into a digital audio system - eg. the output of a microphone - possess frequency components above 20 kHz. With a sampling frequency of 40 kHz, the frequencies above 20 kHz must be attenuated by an analogue anti aliasing (low pass) filter with a brickwall slope to prevent them from entering the audible hearing range.
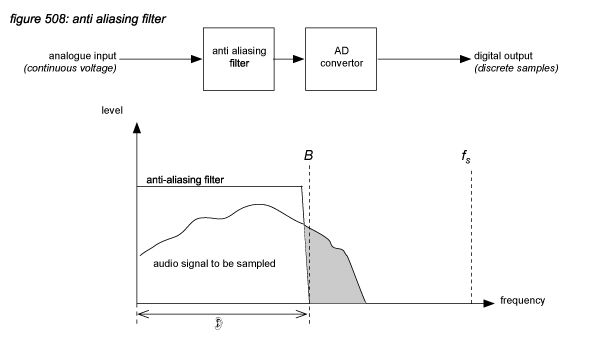
In the analogue world, its impossible to design a brickwall filter with infinitive roll-off. The solution is to select a slightly higher sampling frequency to allow a less steep roll-off of the low pass filter. But still, a high roll-off slope creates phase shifts in the high frequency range - so to ensure phase linearity in the analogue anti aliasing filter, the sampling rate should be as high as possible. With the conception of the CD standard, Philips and Sony settled on a 44.1 kHz sampling rate as the optimal compromise between analogue filter design and CD storage capacity - leaving only 2 kHz for the roll-off, so the analogue filters on the first CD players where very tight designs. For broadcast and live applications, 48 kHz became the standard, allowing for slightly less tight anti aliasing filter designs. Some years later, with the availability of faster digital processing, the sampling rate could be set to a much higher level to allow much simpler analogue filters to be used - the processing to prevent aliasing could then be performed in the digital domain. This concept is called ‘oversampling’, now used by virtually all manufacturers of A/D and D/A converters(*5P).
All professional digital audio systems on the market today are capable of using a sample rate of at least 44.1 kHz with oversampling A/D and D/A converters, ensuring accurate full bandwidth conversion and processing of audio signals.
5.4 Timing issues
Signal propagation through cables happens at close to light speed - 299.792.458 meters per second(*5Q). The speed is limited by the cable’s insulation - an unshielded cable will transfer audio signals at approximately 96% of the light speed, a coaxial cable at appr. 66%. Because of this limitation, a 100 meter coaxial cable will induce approximately 0,5 microseconds delay. Semiconductors also induce delays - a 74HC4053 analogue switch (an integrated circuit used in many remote-controlled head amps) typically adds 4 nanoseconds delay to the signal path(*5R).
Analogue signal distribution and processing circuits operate with this limitation - which normally does not affect audio quality unless for example the cabling spans more than 1,8 kilometers, lifting the delay above the 6 microseconds hearing limit.
Digital systems however operate at much lower speeds because signals are chopped in samples and then distributed and processed sample-by-sample - which requires a multiple of the sample time involved. For digital audio systems with a 48kHz sampling rate, the sample time is 20.8 microseconds - well above the 6 microseconds hearing limit. Where dynamic range and frequency range of digital audio systems have developed to span almost outside the reach of the human auditory system, time performance is a bottleneck that can not be solved. Instead, system designers and operators will have to study the time performance of their digital systems in detail, and take countermeasures to limit the consequences for audio quality as much as they can for every individual system design.
With analogue systems, engineers only had to concern themselves with the acoustic timing issues of microphone and speaker placement. With the introduction of digital (networked) audio systems, this task is expanded with the concern for digital timing or latency. The acoustic and digital timing issues basically cause the same effects, requiring a combined approach to achieve a high audio quality.
The following issues concerning time performance of digital audio systems will be covered in the following chapters:
table 501: timing issues in digital systems
issue
typical delay (48kHz)
cause
network latency
1 ms
one pass through a networked distribution system
processing latency
1 ms
a digital mixer’s signal processing
conversion latency
0.5 ms
AD or D/A conversion
clock phase
0.01 ms
synchronisation and receiver circuits
jitter
0.000005 ms
PLL, electronic circuits, cabling, network
5.5 Absolute latency
The latency of a signal chain in a typical networked audio system at a sampling frequency of 48 kHz is around 4 milliseconds. The main factors are distribution latency, DSP latency and AD/DA latency. In recording studio’s with isolated control rooms - where the listener never hears the sound source directly - latency is not a problem at all. If the listener can see the sound source (but not hear it), a latency of up to 20 milliseconds (corresponding with the PAL video frame rate of 50 Hz) is allowed before video and audio synchronisation mismatch can be detected - mainly due to the slow reaction time of the eyes and the visual cortex in the human brain.
In live audio systems however, the audio signals radiated by the sound sources are often mixed with the processed output of the audio system - causing problems if the two signals have similar amplitude. With high latencies, a ‘delay’ is perceived by listeners and performers, which is specially inconvenient for musicians because it disturbs musical timing. Low latencies cause comb filtering, disturbing timbre and pitch. This problem is most prominent for vocal performances where a singer hears his or her own voice acoustically and through bone conduction, as well as through a monitor system.
For in-ear monitoring, latencies of more than 5 milliseconds might cause single sounds to be heard as two separate audio signals, disturbing musical timing. Below 5 milliseconds, latency causes comb filtering - which is also a problem, but can be adapted to by experienced performers. As a rule of thumb, high quality vocalist in-ear monitoring ideally requires a system latency (from microphone input to headphone output) of less than 5 milliseconds, preferably lower.
For monitoring systems using loudspeakers, the issue is less significant because the acoustic path from the loudspeaker to the ear is included in the signal chain, adding about 4 milliseconds or more acoustic delay. Although the latency is noticeable, because of the acoustic reflections the comb filter effect is less audible.
For Front Of House (FOH) Public Address (PA) speaker systems, the absolute latency of a networked system is much less significant because the distance of the listener to the sound source normally is several meters, adding tens of milliseconds acoustic delay - making the system’s latency less significant. Also, FOH PA speaker systems normally are situated in front of the performers to prevent feedback, in some cases compensating the latency difference between system PA output and the source’s direct sound for the audience. Figure 510 and table 502 show a typical networked live audio system and the latencies and acoustic delays that occur. Table 503 shows an average typical latency perception of musicians (pianist, vocalist, guitarist) analysed in numerous test sessions by Yamaha.
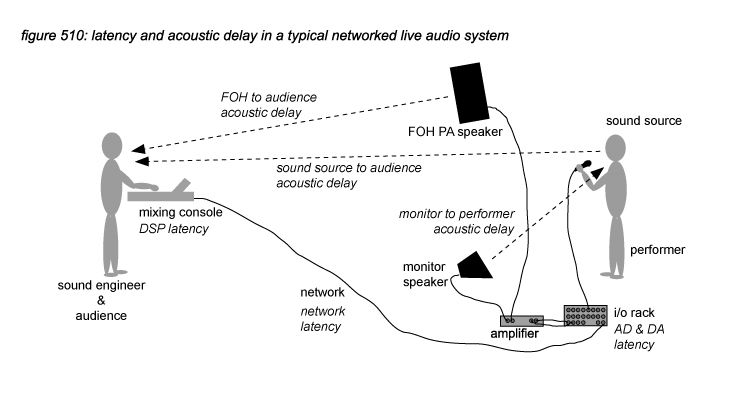
table 502: latency and acoustic delay in a typical networked live audio system
signal path latency & acoustic delay (ms)
in-ear to performer
monitor speaker to performer
PA speaker to audience
sound source to audience
A/D conversion
0.5
0.5
0.5
n/a
network i/o rack -> FOH
1
1
1
n/a
DSP
1
1
1
n/a
network FOH -> i/o rack
1
1
1
n/a
D/A conversion
0.5
0.5
0.5
n/a
monitor speaker @ 2m*
n/a
6
n/a
n/a
PA speaker @ 20m*
n/a
n/a
58
n/a
sound source @ 23m*
n/a
n/a
n/a
67
total latency (ms)
4
10
62
67
table 503: average monitor system’s absolute latency perception by musicians (Pianist, Vocalist, Guitarist)
signal path latency
for in-ear monitor systems
for floor monitor systems
1.15 - 2 ms
Playable without any big problem.
Playable.
2 - 5 ms
Playable, however tone colour is changed.
Playable.
5 - 10 ms
Playing starts to become difficult. Latency is noticeable.
Playable. Although latency is noticeable, it is perceived as ambience.
>10 ms
Impossible to play, the delay is too obvious.
Impossible to play, the delay is too obvious.
5.6 Relative latency
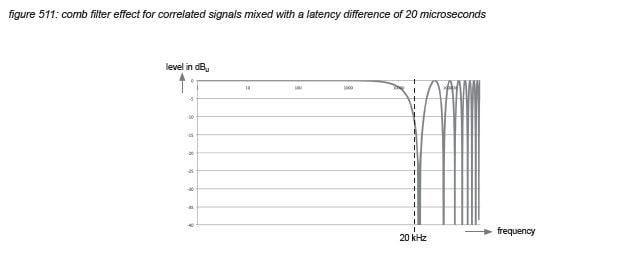
Similar to the design challenge of coping with acoustic delays in speaker systems, latency in networked systems cause timing and comb filtering problems if multiple signal paths exist from sound source to listener. An example is a stereo overhead of a drum kit, where a certain portion of the outputs of the left and right microphones contain identical - correlated - signals. When these signals arrive at a listener with different latencies, the timing difference as well as the comb filtering can be detected by listeners - even for very small latencies down to 6 microseconds.
Figure 511 shows the comb filter effect caused by mixing two identical signals with a latency difference of 20 microseconds (roughly one sample at 48 kHz). Although the cancellation frequency of the comb filter effect lies at 24 kHz - above the hearing limit of 20 kHz, the slope already starts to attenuate frequencies within the hearing range, so the effect can be detected by listeners independent from the detection of the time difference itself. At 20 kHz, the attenuation is -10 dB. For latency differences of two samples or more, the cancellation frequency moves inside the hearing range causing clearly audible interference patterns - similar to the interference patterns created by the acoustic delay when using multiple loudspeakers.
Many digital mixing consoles and digital signal processors have delays built in to manipulate latency - for example to correct relative latency problems.
Networks (timing protocol) and DSP processes (latency compensation) have built-in latency correction mechanisms that align latencies of all signal paths in the system. However, it is important to remember that this is only valid for the default path - eg. a default signal chain in a mixer, or a single pass through a network. If an external process is inserted in the signal path, eg. a graphic equalizer, the latency of that signal path increases with the latency of the graphic equalizer relative to all other signal paths in the mixer. If the equalizer is connected through a network, the network latency has to be added as well.
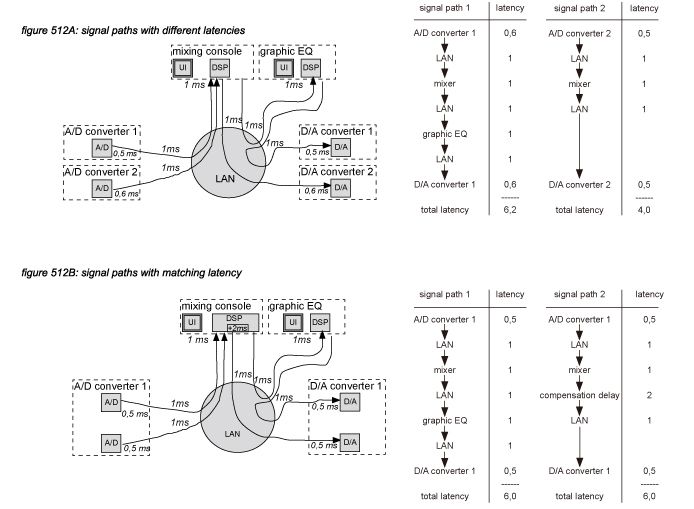
Another possible cause for latency differences is the use of different digital components for correlated signals. Different components - including A/D and D/A converters - may add different latencies to the signal paths. In general, it is advisable to route correlated signals through the same type of components - preferably only one.
Figure 512A shows a system where 0,2 milliseconds (10 samples) latency difference is caused by using different A/D and D/A converters, and another 2 milliseconds (100 samples) is added by the inserted graphic equalizer and the extra pass through the network. Figure 512B shows the same application using the same A/D and D/A converter devices for both signal paths, and applying a manual compensation delay in the mixing console output for signal path 2, resulting in the same latency for both signal paths.
5.7 Word clock
All digital audio devices need a word clock to trigger all the device’s digital audio processes. If a device is used as a stand-alone component - eg. a CD player, or a digital mixing console used with only analogue connections - then the internal clock is most often a crystal oscillator, providing a stable and accurate clock signal. However, as soon as two or more digital audio devices are used in a system, their internal word clocks need to use the same frequency to assure that all samples sent by one device are actually received by the other. If for example one device’s internal word clock is running at 48,000 Hz, and it sends its data to a second device running at 47,999 Hz, each second one sample will go missing, causing a distortion in the audio signal. To prevent this, all devices in a digital audio system have to synchronize to a single, common ‘master’ word clock source - which can be any of the devices in the network, or a separate external word clock generator.
Digital audio devices can not simply be connected directly to a master word clock - any disruption in the master word clock (eg. induced by electronic circuit noise, power supply noise) or its cabling (time delays, electromagnetic interference) can spread around the system to all other devices, with the possibility to cause unstable situations. To ensure stability in a digital system, all devices in it are synchronised to the master word clock through Phase Lock Loop (PLL) circuits, following only slow changes in the master clock’s frequency, but ignoring fast disruptions. PLL’s use a Voltage Controlled Oscillator (VCO) or a more accurate Crystal VCO (VCXO) to generate the device’s internal sample clock to drive all its processes, with the frequency kept in phase with the master word clock by a phase comparator circuit that only follows the slow phase changes. VCXO PLL designs are suited for stable studio environments because they are very accurate. The downside of VCXO’s is that they can only support a limited range of external frequencies - losing synchronisation if the master clock’s frequency runs out of the specified range. Also, some VCXO based PLL designs can take a long time to synchronise. In broadcast and live systems, a broad range of sample rates have to be supported to enable the use of a variety of external synchronisation sources (eg. time code regenerated word clocks, digital tape recorders), with a fast synchronisation time to ensure a quick recovery in redundant systems. For this reason, VCO based PLL’s are often used. With the introduction of the Precision Time Protocol (PTP) in AVB networks, also used by Dante, a part of the synchronisation is taken care of by the network interfaces.
From a functionality point of view, synchronisation signals are distributed separately from the audio data. Packet switching network protocols, such as CobraNet and Dante, distribute the synchronisation signal physically on the same cabling as the audio packets, but logically as separate data packets (figure 513a). Serial digital protocols such as AES3 (AES/EBU), AES10 (MADI), and packet streaming network protocols such as EtherSound, include the synchronisation signal in the audio stream (figure 513b). At any time, the designer of the system can decide to use an alternative word clock distribution using an external master word clock generator in order to synchronise to an external source, for example a video signal. An external word clock can be connected to just one device in the networked audio system - distributed to all other devices through the original distribution method (figure 513c), or to all devices individually (figure 513d). Special care should be taken for live systems with long cable runs as the word clock signals transported over coaxial cables are prone to degeneration, potentially causing synchronisation instabilities in a system.
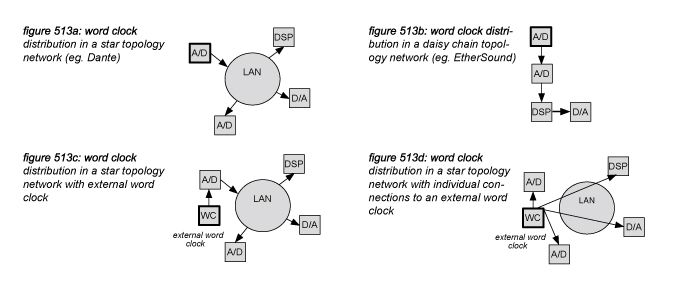
5.8 Clock phase
All processes in a digital audio system are triggered by a common synchronisation signal: the master word clock. The rising edge of the word clock signal triggers all processes in the system to happen simultaneously: A/D and D/A conversion, DSP processing and the transmission and receiving of audio data (transport).
For packet switching audio protocols using star topology networks (such as Cobranet, Dante, AVB), the distribution of the synchronisation information uses separately transmitted timing packets, ensuring that all devices in the network receive their clock within a fraction of the sample time (20.8 microseconds at 48 kHz). This assures for example that all AD samples in the system end up in the same sample slot. But for streaming audio protocols using daisy chain or ring topologies it is different: the clock information is represented by the audio data packets, so the length of the daisy chain or ring determines the clock phase caused by the network. For example, Ether- Sound adds 1,4 microseconds latency per node - accumulating to higher values when many nodes are used.
Additionally, a device that synchronises to an incoming synchronisation signal needs some time to do so. Digital circuit designers focus primarily on matching the incoming synchronisation signal’s frequency as stable, flexible and fast as possible, rather than on the clock phase. As a result, digital audio devices on the professional audio market all have a different clock phase, which is almost never documented in the product specifications. Figure 514 presents a system that uses two different A/D converters that have a different clock phase: the samples are taken and sent to a digital mixer at a different time. As soon as the samples arrive in a digital mixer, the receiver circuit in the mixer will buffer and align the samples, mixing them as if they were taken at the same time, introducing a latency difference between the samples that is smaller than one sample. Because the latency difference caused by differences in clock phase are smaller than one sample, digital delays can not be used to compensate them - the minimum delay time available in a digital signal processor or mixer is one sample.
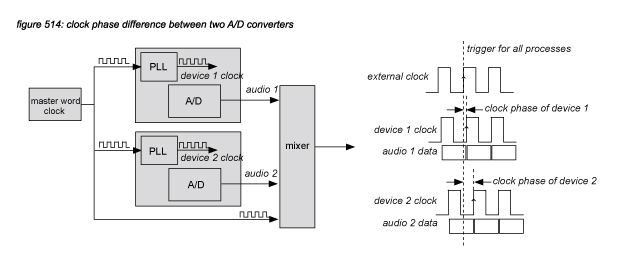
The compensation of clock phase differences can not be included in the system engineering phase of a project because almost all digital audio devices on the market do not specify clock phase delay. Conveniently, in practise, acoustically tuning a system (placing the microphones and speakers) already includes the compensation of all acoustical delays as well as clock phase; aligning all signal paths to produce a satisfactory audio quality and sound quality according to the system technician. As it is important not to move microphones and loudspeakers after a system has been acoustically tuned, it is of equal importance not to change routing and word clock distribution. Some ‘internal/external clock’ comparison listening sessions change the word clock distribution topology manually. The resulting differences in sound are often attributed to jitter performance, while in some cases clock phase changes might have been more significant: a clock phase difference close to half a sample can already be detected both in timing and comb filter effect (see also figure 511 in chapter 5.6).
5.9 Temporal resolution
Chapter 5.3 describes a digital audio system with a sample frequency of 48 kHz to be able to accurately represent frequencies up to 20 kHz. For continuous signals, this frequency is the limit of the human hearing system. But most audio signals are discontinuous, with constantly changing level and frequency spectrum - with the human auditory system being capable of detecting changes down to 6 microseconds.
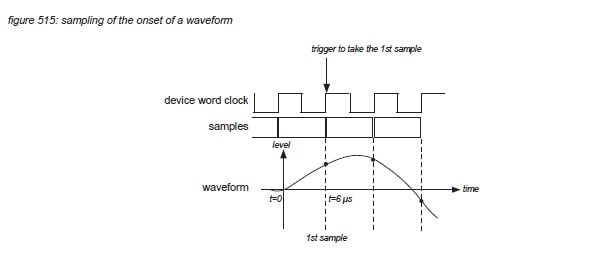
To also accurately reproduce changes in a signal’s frequency spectrum with a temporal resolution down to 6 microseconds, the sampling rate of a digital audio system must operate at a minimum of the reciprocal of 6 microseconds = 166 kHz. Figure 515 presents the sampling of an audio signal that starts at t = 0, and reaches a detectable level at t = 6 microseconds. To capture the onset of the waveform, the sample time must be at least 6 microseconds.
In the professional live audio field, a 48 kHz sampling rate is adopted as standard, with some devices supporting multiples of this rate: 96khz and 192kHz. (Some devices also support 44.1 khz and 88.2 kHz for compatibility with the music recording field, eg. the Compact Disk). However, apart from the temporal resolution of a digital part of an audio system, the temporal characteristics of the electro-acoustic components of a system also have to be considered. In general, only very high quality speaker systems specially designed for use in a music studio are capable of reproducing temporal resolutions down to 6 microseconds assumed that the listener is situated on-axis of the loudspeakers (the sweet spot). For the average high quality studio speaker systems, a temporal resolution of 10 microseconds might be the maximum possible. Live sound reinforcement speaker systems in general can not support such high temporal resolutions for several reasons.
Firstly, high power loudspeakers use large cones, membranes and coils in the transducers - possessing an increasing inertia at higher power ratings. A high inertia causes ‘time smear’ - it takes some time for the transducer to follow the changes posed to the system by the power amplifier’s output voltage. Some loudspeaker manufacturers publish ‘waterfall’ diagrams of the high frequency drivers, providing information about the driver’s response to an impulse - often spanning several milliseconds. The inertia of a driver prevents it from reacting accurately to fast changes.
Secondly, live systems often use multiple loudspeakers to create a wide coverage area, contradictory to the concept of creating a sweet spot. The electro-acoustic designer of such a system will do what ever is possible to minimize the interference patterns of such a system, but the result will always have interference on all listening positions that is more significant than the temporal resolution of the digital part of the system.
Aside from audio quality parameters, the choice of a sampling rate can also affect the bandwidth - and with it the costs - of a networked audio system. Table 504 on the next page presents the main decision parameters.
As a rule of thumb, 48 kHz is a reasonable choice for most high quality live audio systems. For studio environments and for live systems using very high quality loudspeaker systems with the audience in a carefully designed sweet spot, 96 kHz might be an appropriate choice. Regarding speaker performance, 192 kHz might make sense for demanding studio environments with very high quality speaker systems - with single persons listening exclusively in the system’s sweet spot.
Digital I/O Characteristcs
5.10 Jitter
In any digital audio system, time information is ignored. It is not registered by A/D converters, and it is not passed through the distribution protocol - the packets in AES/EBU bit streams or CobraNet bundles only include level information, not time information. Instead, the sample time is assumed to be reciprocal of the system’s sample frequency - generated by system’s master word clock. Furthermore, it is assumed that all samples are sent - and received - sequentially, and that there are no missing samples. Even the DSP algorithm programmer just assumes that his software will be installed on a system that runs on a certain sampling frequency - eg. filter coefficients are programmed to function correctly at 48 kHz. If the system’s master word clock runs at 47 kHz, the system will probably be perfectly stable, but all filter parameters will be a little off.
All devices in a digital audio system have an internal word clock - most often synchronised to a common external word clock through a PLL circuit. Both the internal word clock signal and the external word clock are pulse trains at a frequency equal to the system’s sample rate that provide a rising edge to trigger all processes in the system.
An ideal word clock will produce a rising edge in constant intervals. But in reality, noise in related electronic circuits (eg. oscillators, buffer amps, PLLs, power supplies) and electromagnetic interference and filtering in cabling will distort the word clock’s waveform - causing the rising edge to come too early or too late, triggering the processes in the digital audio system at the wrong time. The signal that represents the deviation from the ideal time is called jitter. In digital audio products it is normally a noise-shaped signal with an amplitude of several nanoseconds.
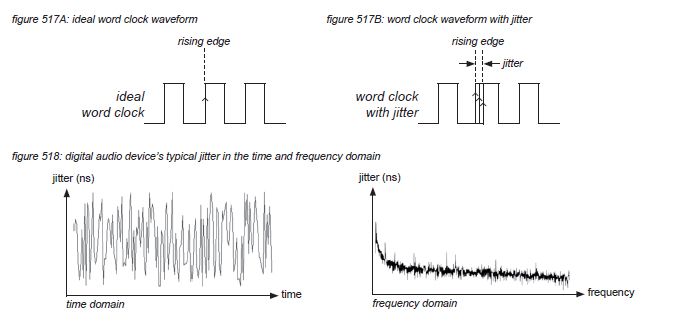
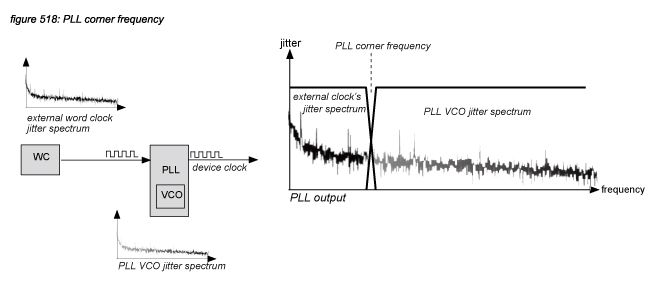
In digital audio systems, all devices synchronise to a common master clock through their PLL circuits. The PLL will follow only the slow changes in phase (low frequencies in the external word clock’s jitter spectrum), and ignore the fast changes - keeping the PLL’s own VCO’s jitter spectrum. The jitter spectrum of the PLL’s output (the device clock) is a mix of the low frequencies of the external word clock’s jitter spectrum, and the high frequencies of the PLL’s VCO jitter spectrum. The frequency where the external jitter starts to get attenuated is called the PLL’s corner frequency. In digital audio devices for live applications, this frequency is normally between 10 Hz and 1 kHz with a relatively short synchronisation time (the time it takes for the PLL to synchronise to a new word clock). For studio equipment this frequency can be much lower - offering a higher immunity for external word clock quality, but with a longer synchronisation time.
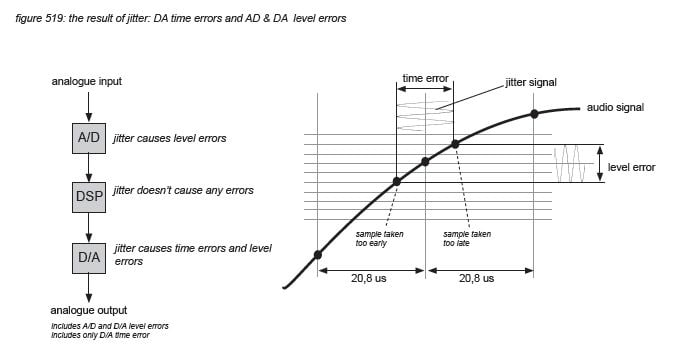
Jitter in a device’s word clock is not a problem if the device only performs digital processes - a MAC operation in a DSP core performed a little earlier or later than scheduled gives exactly the same result. In digital audio systems, jitter only causes problems with A/D and D/A conversion. Figure 519 shows that a sample being taken too early or too late: the jitter timing error - results in the wrong value: the jitter level error. As time information is ignored by the DSP processes and distribution of a digital audio system, only the level errors of an A/D converter are passed to the system’s processes. At D/A converters however, samples being output too early or too late distort the audio signal in level and in timing. The listener to the system hears both A/D and D/A converter jitter level errors, but only the D/A converter’s timing error.
All major mixing consoles on the market today specify a jitter peak value of the internal PLL’s output of 5 nanoseconds. This value is more than a factor 1000 under the human hearing threshold of 6 microseconds - we propose to assume that such small time errors can not be detected by the human auditory system.
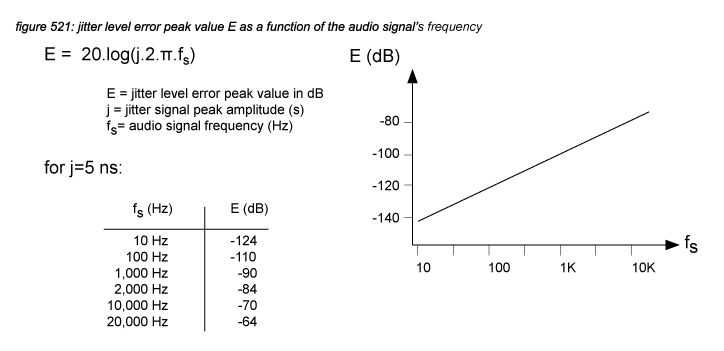
Jitter level errors generated by this time error however fall in the audible range of the human auditory system. For small jitter time errors, with a sine wave audio signal A(t) and a noise shaped jitter signal J(t) with bandwidth B, the jitter level error E(t) is generated as presented in figure 520(*5S).
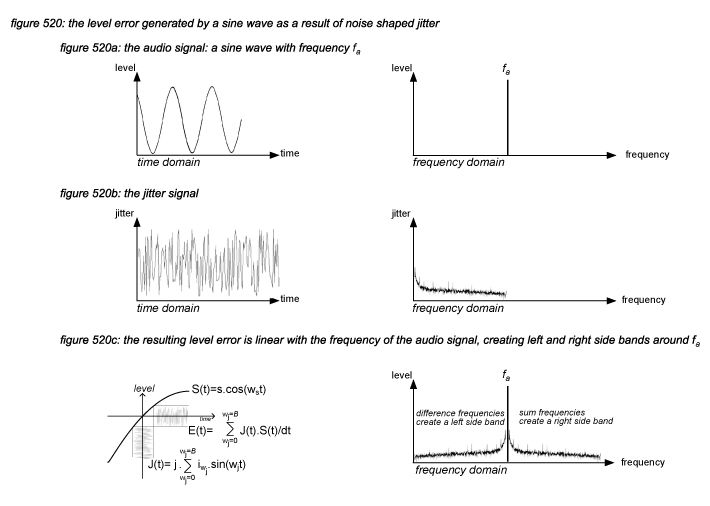
The result for a single frequency component in the audio signal is presented in figure 520c. For sinusoidal jitter, the term J(t).S(t)/dt can be represented by the expression E(t) = s.j.ws.{1/2 sin((ws+wj)t)+ 1/2 sin((ws-wj)t)}. Adding up all frequencies in the jitter spectrum, it can be shown that the jitter spectrum folds to the left and the right of the audio frequency - this ‘jitter noise picture’ can be produced by any FFT analyser connected to a digital audio device that processes a high frequency sine wave. Repeating this calculation for every frequency component in a real life audio signal gives the resulting total jitter level error. The overall peak value of the jitter level error (E) is linear with the derivative of the audio signal: the higher the frequency, the faster the signal changes over time, the higher the jitter level error. The worst case is a 20kHz sine wave, generating a jitter level error at a 64dB lower level. As most energy in real life audio signals is in the low frequencies, the majority of the generated jitter level errors will be far below -64dB.
Low frequency jitter correlation
As PLL circuits follow the frequencies in the master word clock’s jitter spectrum below the PLL’s corner frequency, the low frequency jitter in all devices in a digital audio system will be the same - or correlated. Theoretically, for a signal that is sampled by an A/D converter and then directly reproduced by a D/A converter, all jitter level errors generated by the A/D converter will be cancelled by the jitter level errors generated by the D/A converter, so there is no jitter level error noise. In real life there is always latency between inputs and outputs, causing the jitter signals to become less correlated for high frequencies. If the latency between input and output increases, then the frequency at which the jitter is correlated will decrease. At a system latency of 2 milliseconds, the correlation ends at about 40 Hz - this means that in live systems, low frequency jitter (that has the highest energy) is automatically suppressed, but high frequency jitter in A/D converters and D/A converters just add up. In music production systems - where the audio signals are stored on a hard disk, posing a latency of at least a few seconds - and of course in playback systems where the latency can grow up to several years between the production and the purchase of a CD or DVD, the low frequency jitter signals are no longer correlated and all jitter level errors will add up.
For packet switching network protocols using the Precision Time Protocol*5T (PTP), such as Dante and AVB, the synchronisation is partly covered by the receiver’s FPGA logic, adjusting a local oscillator to run in sync with up to 10 synchronisation packets per second. This means that the equivalent corner frequency of a PTP receiver is under 10Hz - correlating only for very low frequencies. In such systems, the influence of an external wordclock distributed through low latency networks as in figure 513c is not significant.
audibility of jitter
Assuming a 0dBfs sine wave audio signal with a frequency of 10kHz as a worst case scenario, a jitter signal with a peak level of 5ns will generate a combined A/D and D/A jitter noise peak level of:
EA/D+D/A = 20.log(2.5.10-92.π.10.103) = -64dBfs
When exposed to listeners without the audio signal present, this would be clearly audible. However, in real life jitter noise only occurs with the audio signal in place, and in that case masking occurs: the jitter noise close to the audio signal frequency components will be inaudible, so the average audio signal’s spectrum will mask a significant portion of the jitter noise.
Note that the predicted level is the jitter noise peak level generated by 0dBfs audio signals. In real life, the average RMS level of jitter noise will be lowered by many dB’s because of the audio program’s crest factor and the system’s safety level margins used by the sound engineer. Music with a crest factor of 10dB played through a digital audio system with a safety level margin of 10dB will then generate jitter noise below -84dBfs.
The audibility of jitter is a popular topic on internet forums. Often a stand-alone digital mixing console is used in a listening session, toggling between its internal clock and external clock. In these comparisons it is important to know that such comparison sessions only work with a stand-alone device. If any other digital device is connected to the mixer, then clock phase might play a more significant role in the comparison results than jitter.
In uncontrolled tests, many subjective and non-auditory sensations have a significant influence on the result. More details on quality assessment methods are presented in chapter 9.
In multiple clinical tests, the perception threshold of jitter has been reported to lie between 10 nanoseconds(* 5U) for sinusoidal jitter and 250 nanoseconds(* 5V) for noise shaped jitter - with actual noise shaped jitter levels in popular digital mixing consoles being below 10 nanoseconds.







* speed of sound = 343 m/s